Overview

In this project we implement some of the components involved in creating cloth simulations. Using a system of point masses and springs, we are able to realistically replicate a piece of cloth's behavior in the real world by applying forces to each point mass and checking for collisions. In Autodesk Maya, cloth simulation is done through their nCloth particle network. It can be used to simulate fabric as well as other surfaces such as balloons and liquids, which are likely created by changing parameters such as the spring constant, mass, friction. I imagine a similar physics-based system may also be used in the simulation of particles such as hair or grass.

Part I: Masses and springs

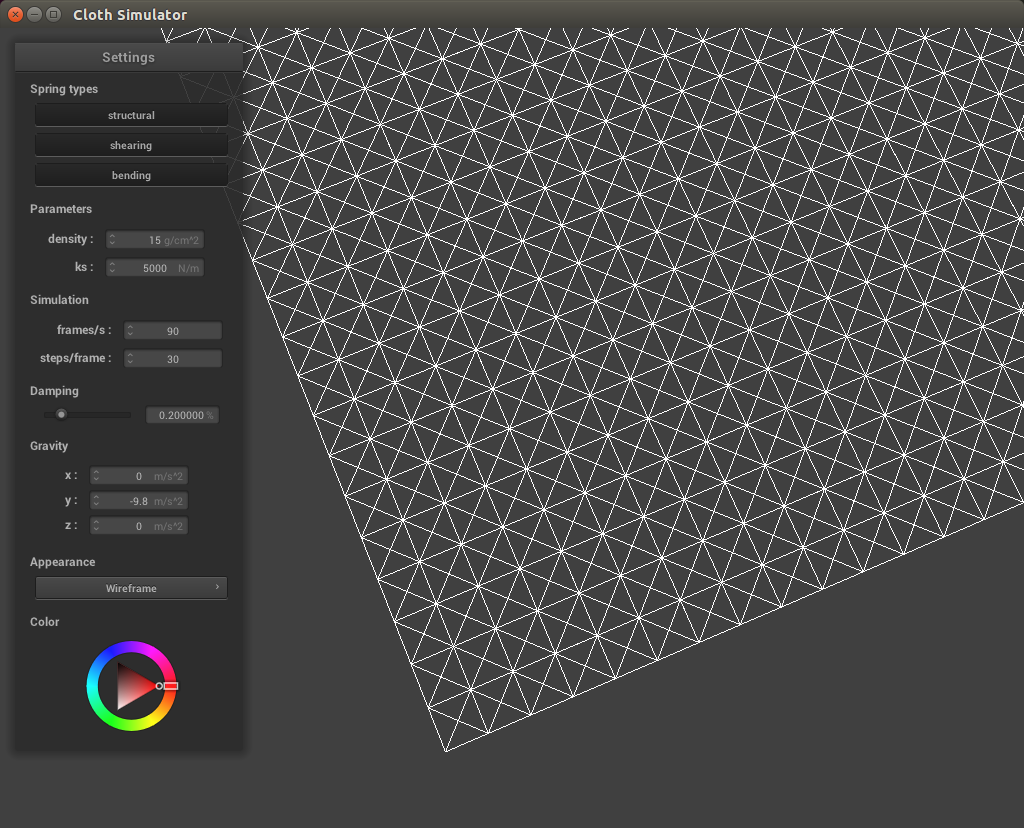
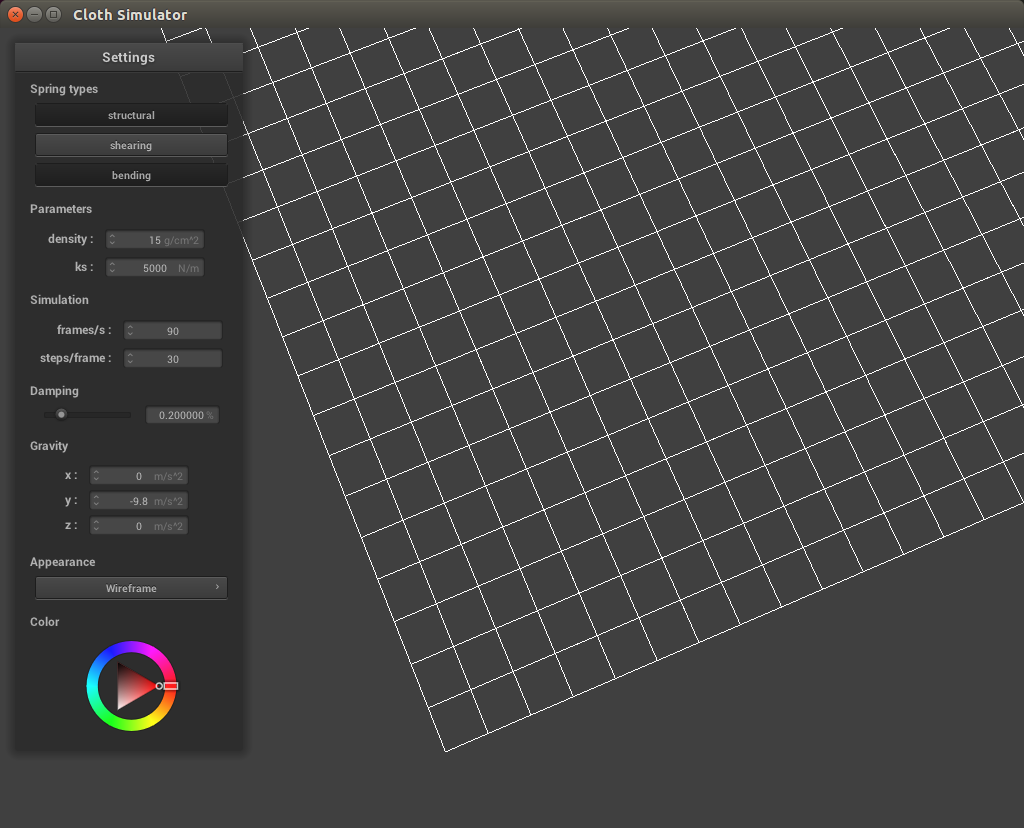
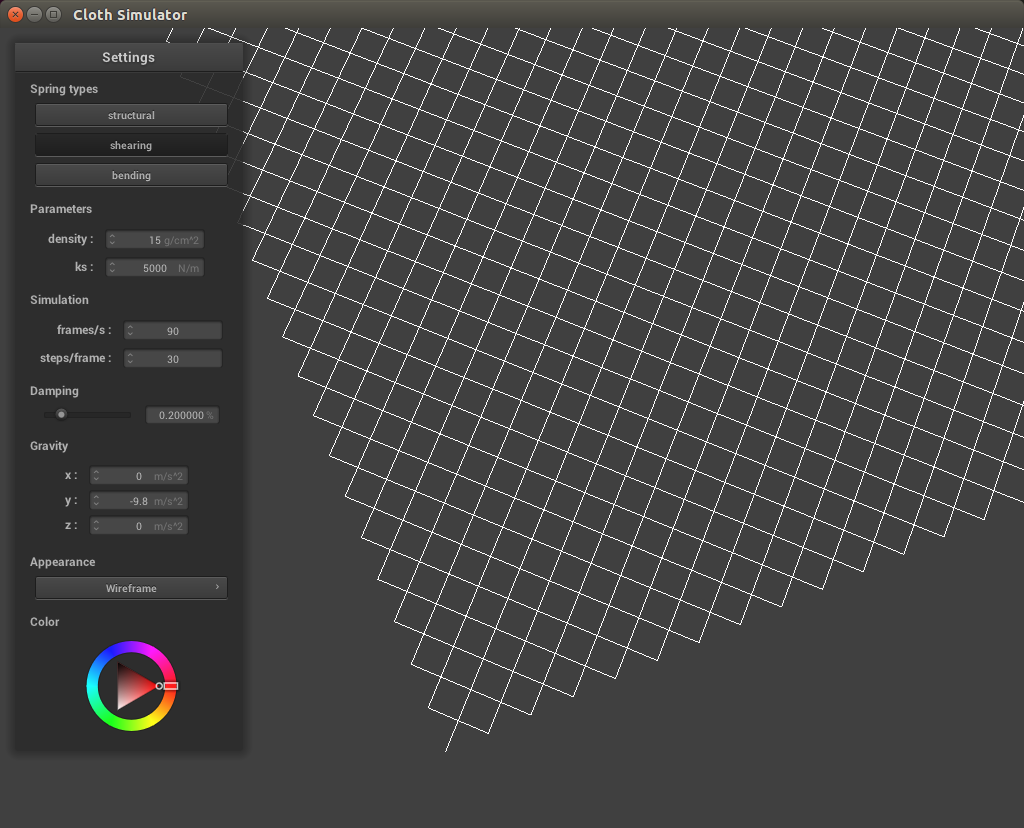
The first step we perform is to set up a grid of point masses and springs, to represent each point in the cloth mesh. We then create springs to apply structural, shearing, and bending constraints to each point mass. Structural constraints were created between a point mass and the point mass on its left as well as immediate above, shearing constraints were created between a point mass and its diagonal upper left as well as diagonal upper right, and bending constraits were created between a point mass and the point mass two away to its right as well as two above it. These constraints were created only if the point masses to be linked were within the bounds of the cloth.

Part 2: Simulation via numerical integration

The next step was to perform a simulation step by using Verlet integration to compute new positions for the point masses. To do this, first we calculated the total force acting on each point mass. This was done in two parts, calculating the external forces and calculating the spring forces. To find the total force from external acceleration, we used Newton's Law (F = ma) along with the cloth's mass and provided external accelerations to compute the external forces applied to each point mass. Computing the spring force required the use of Hooke's Law (F = Ks * X). In this case the change in distance (X) is equal to the distance between the point masses minus the spring's rest length, and we multiply that scalar by the unit vector in the direction from one point to another to get our spring force. We then add this force to the point mass at which our unit vector originates and subtract it from the other.

After calculating the total force on each point mass, we are ready to use Verlet integration to update each of their positions. We use the formula x_t+dt = x_t + (1 - d) * (x_t - x_t-dt) + a_t * dt^2, where d is a damping term and a_t is the acceleration computed from the total force on that point mass divided by the cloth mass.

As an additional step, we also constrained the updated position such that no spring could be more than 10% greater than its rest length at the end of a time step. If we did find a spring that happened to have a length greater than 10% of its rest length, we checked if either point mass on its ends were pinned. If one was, we applied the full correction (the current spring length minus 110% of its rest length) to the non-pinned point mass. Otherwise, we applied half of the correction to both points.

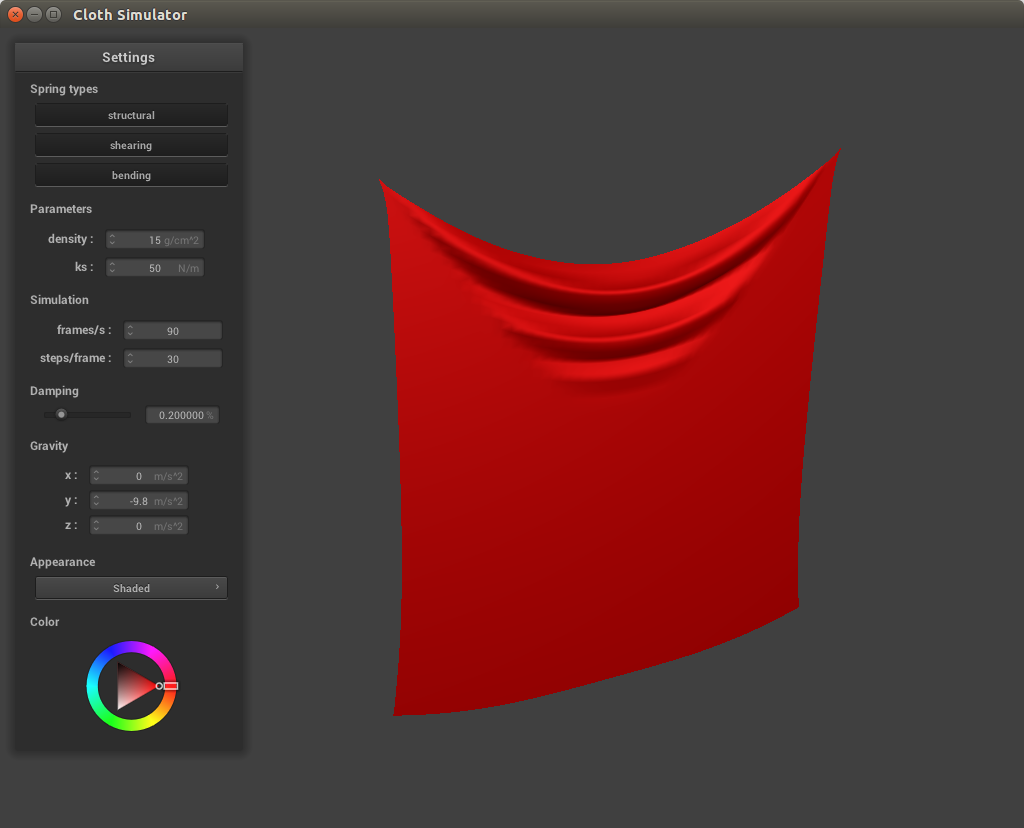
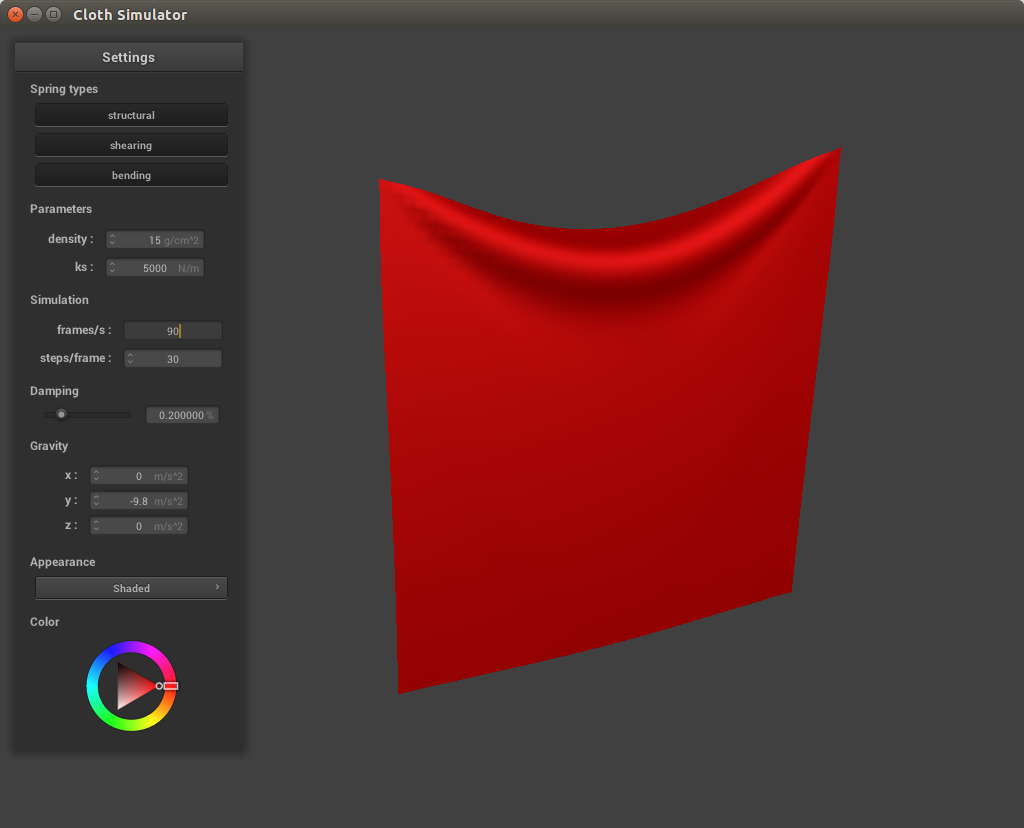
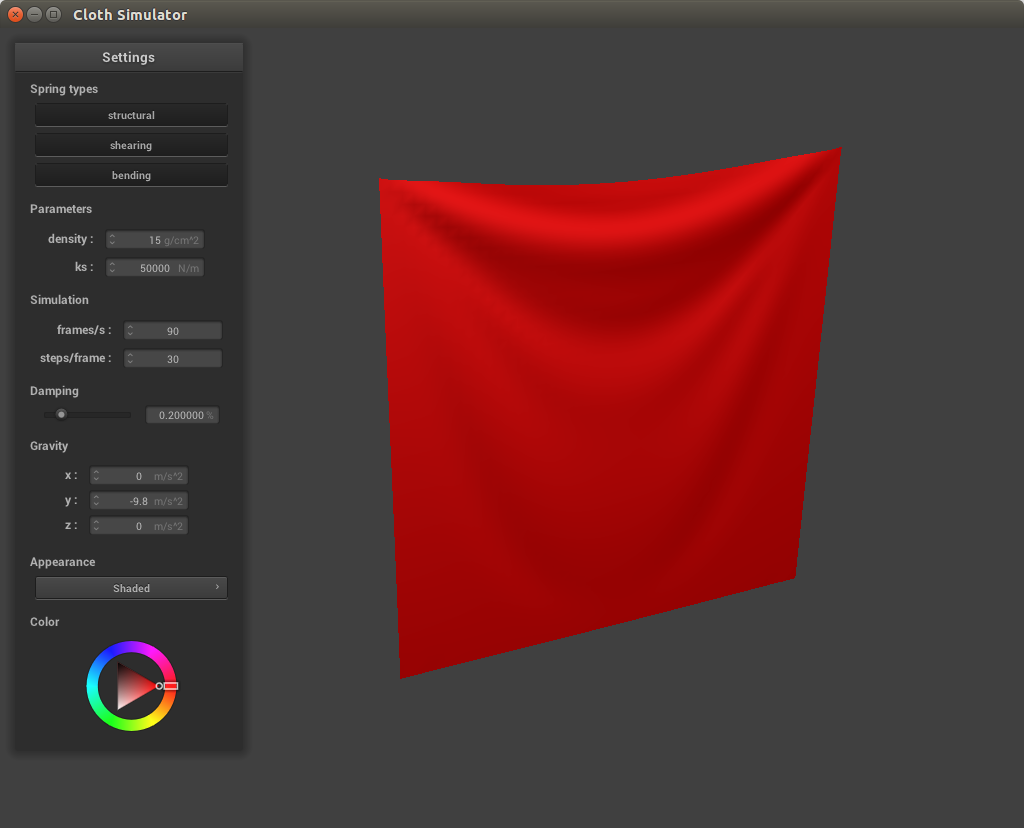
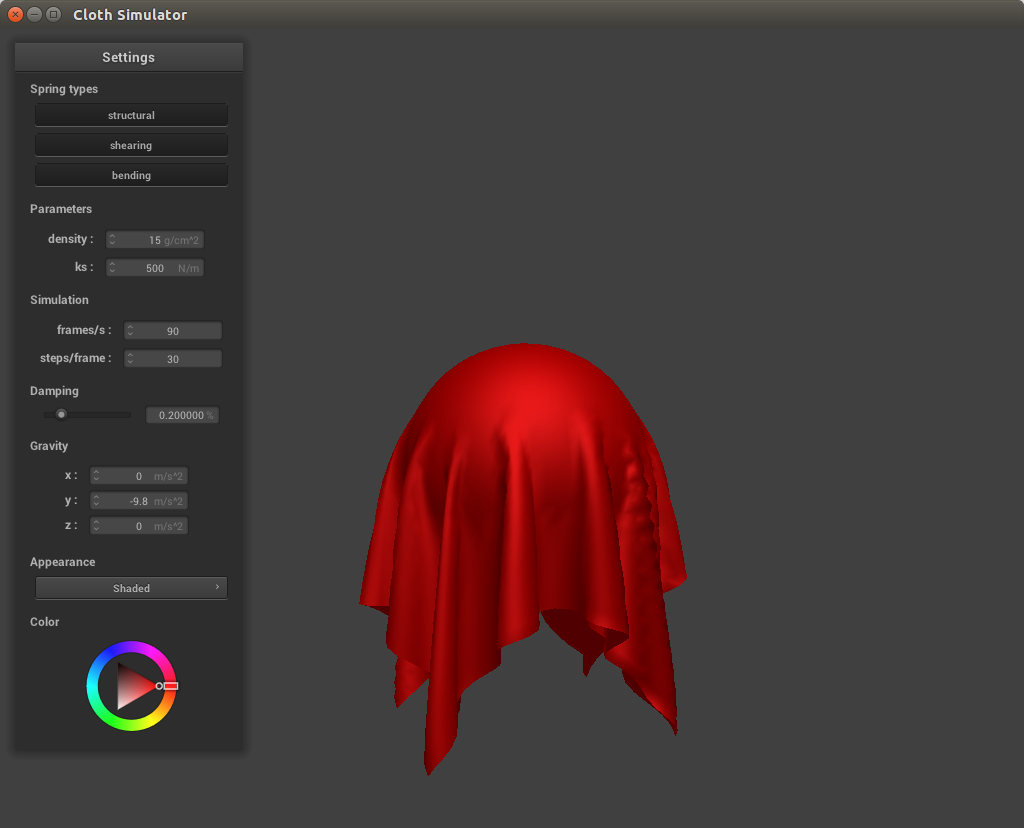
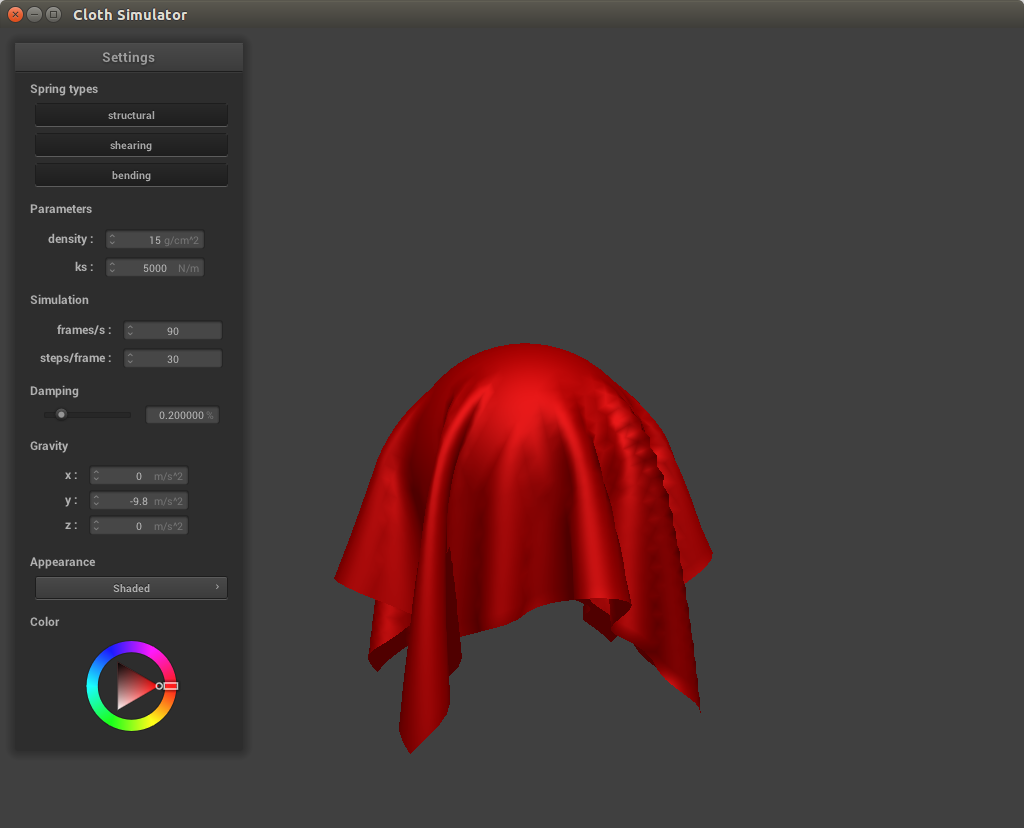
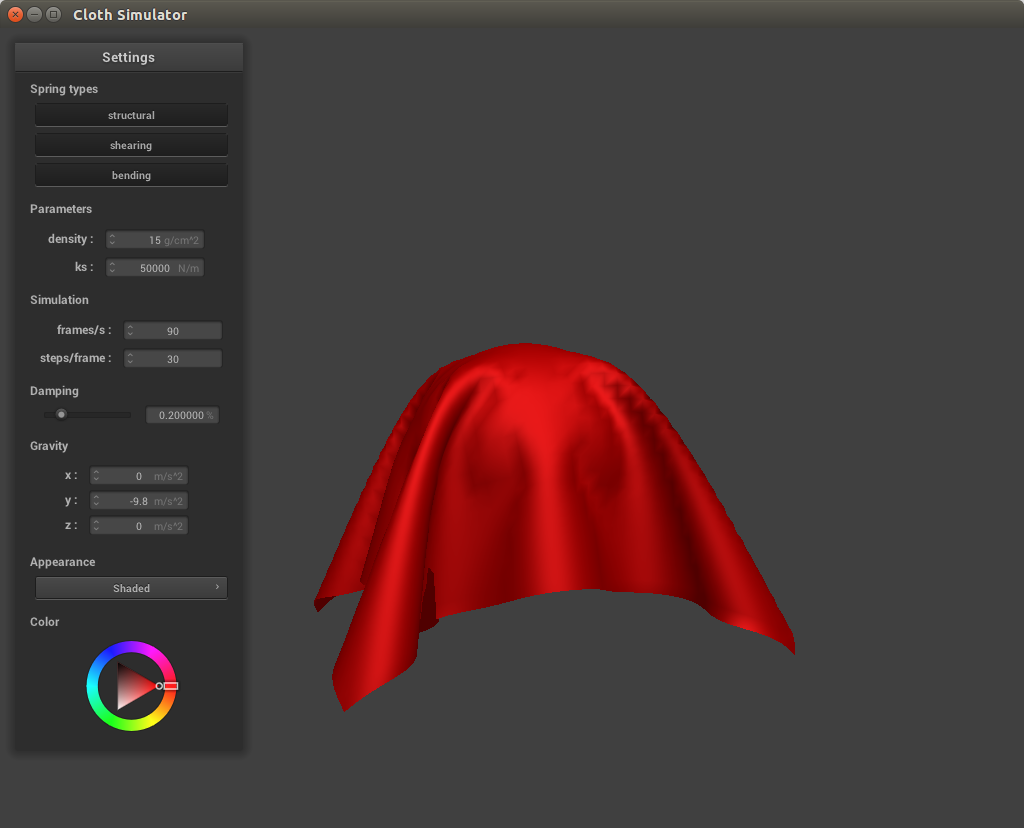
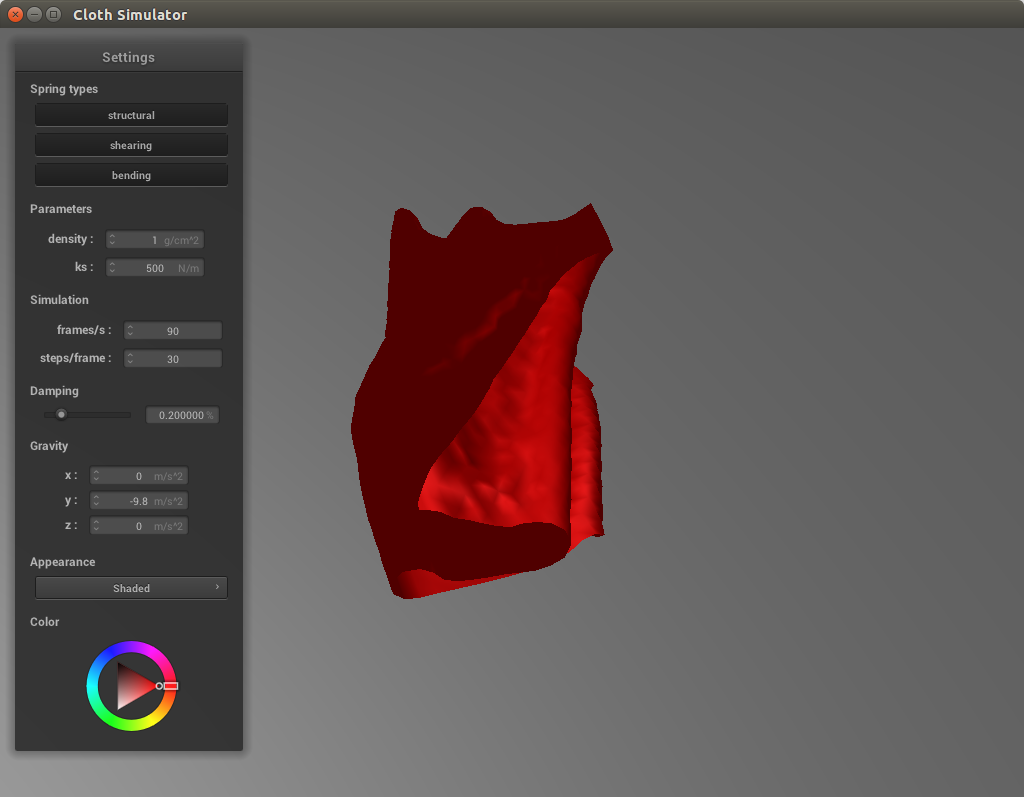
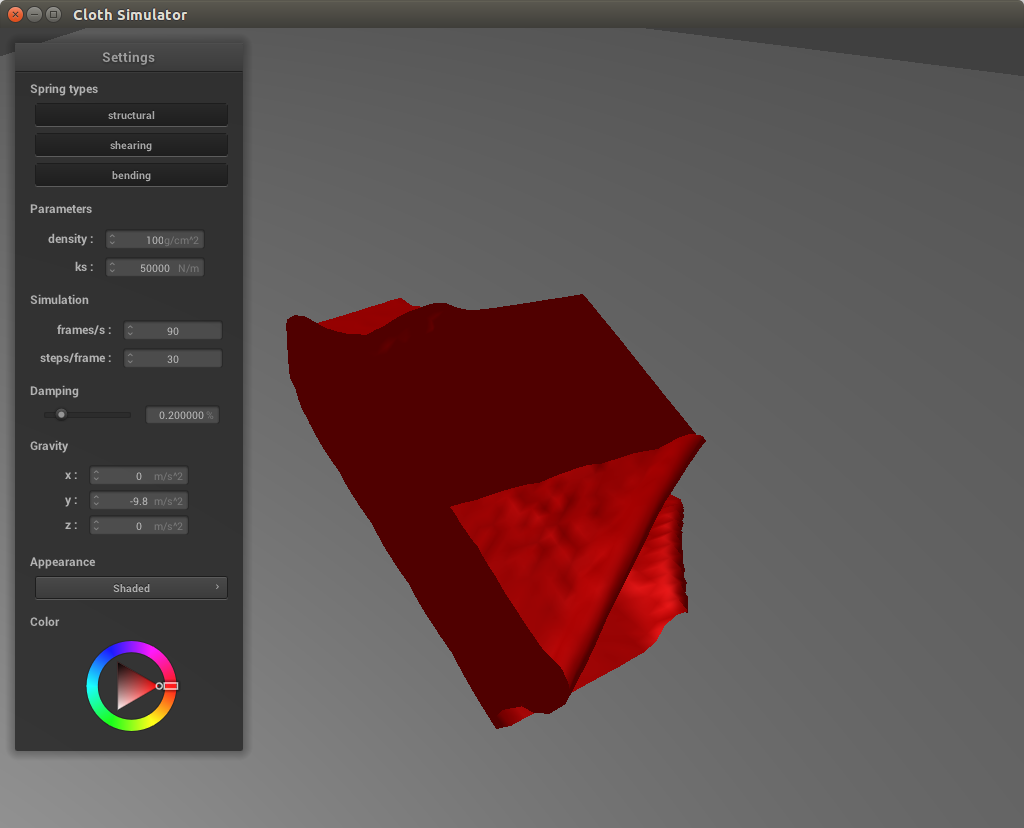
With a low spring constant, there are much more creases in the cloth and it is more slack, having lots of rippling effects while falling. At high spring constants the cloth appears more stable and hangs higher. This is because the spring constant is directly proportional to the strength of the force between each point mass. At higher values the force will be stronger and thus the cloth will be more taut whereas at lower values the forces between the cloth are weaker and thus the cloth is not as tightly held together.

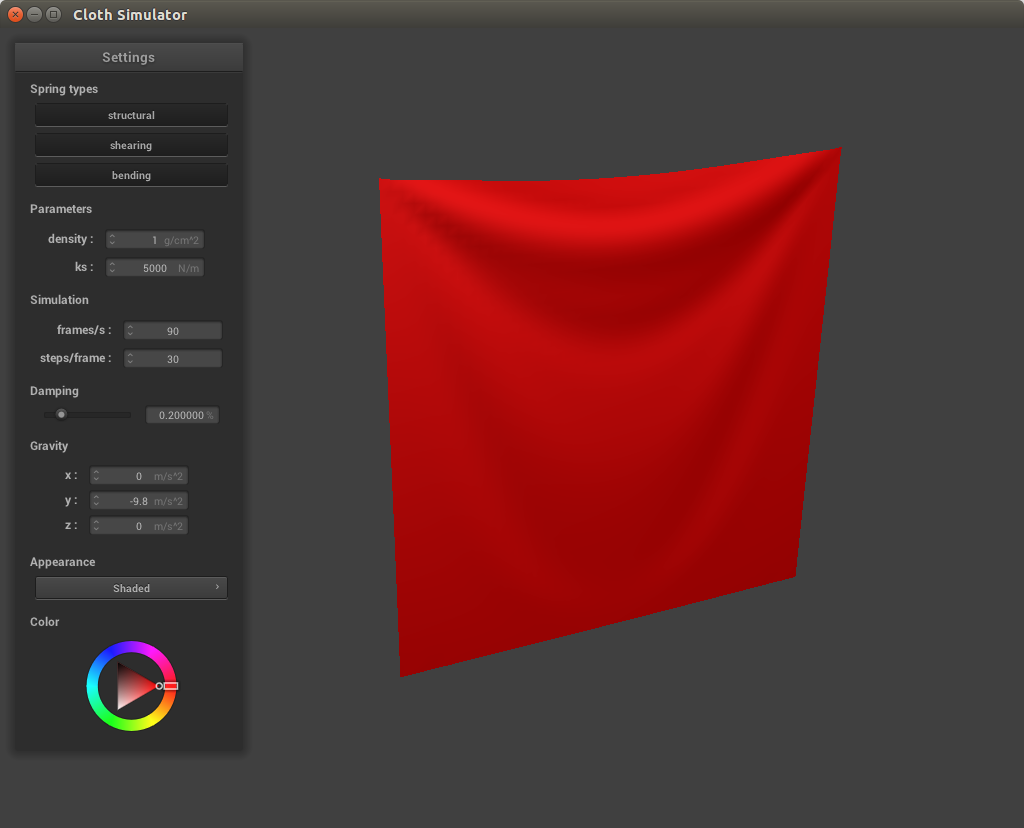
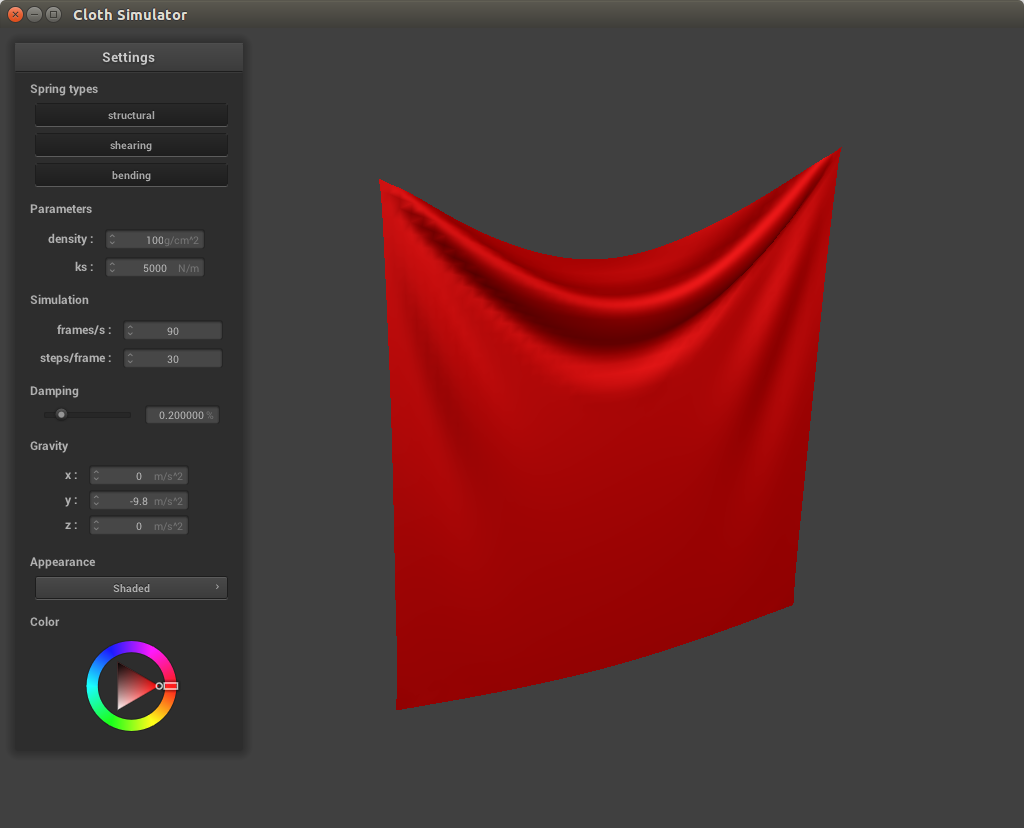
At low density the cloth does not sag as much whereas a higher density results in a deeper crease. This is because density affects the mass of the cloth, and since the area of the cloth has not changed higher density leads to higher mass, resulting in a stronger force of gravity pulling down on the cloth.

At a low damping value the cloth rocks back forth, with a lot of rippling effects, before settling into an equilibrium position. At high damping values the cloth falls very slowly, with little to no changes in its appearance. This is because the damping value determines the energy lost by the cloth system in motion. With high energy loss, the cloth reaches stability much faster, and thus with a high damping value it falls in a relatively slow and rigid fashion. With low damping values the cloth retains much more energy, and thus will swing back and forth to dissipate it before settling.

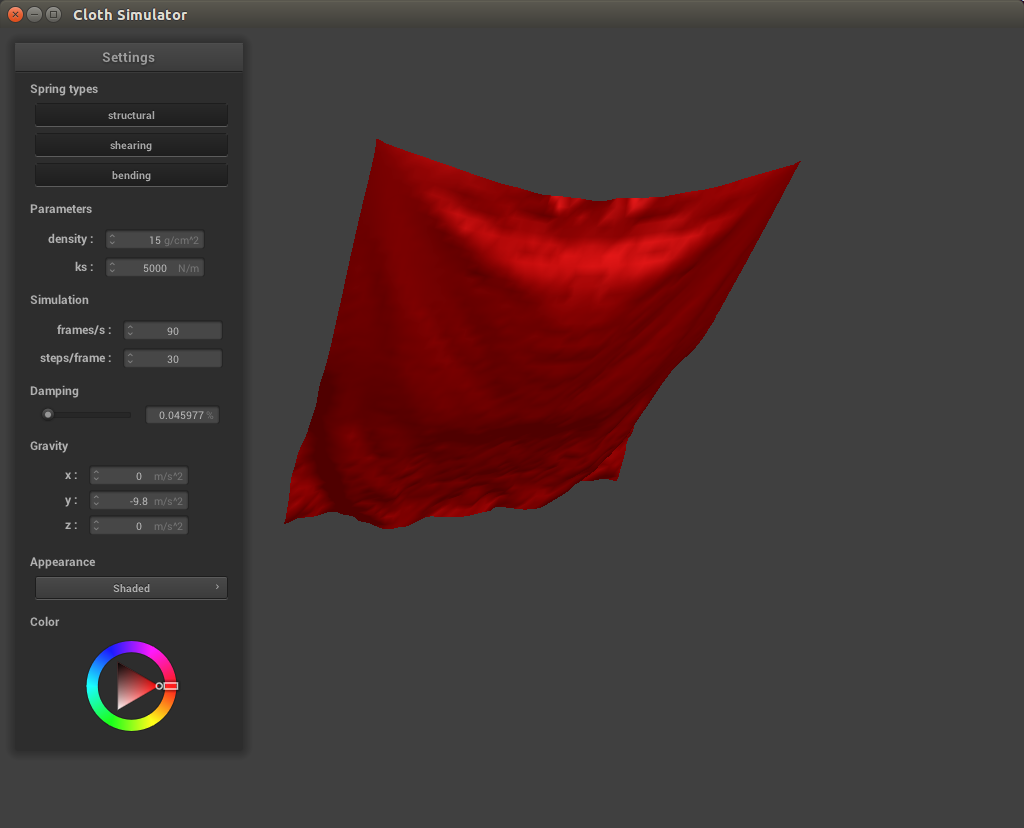
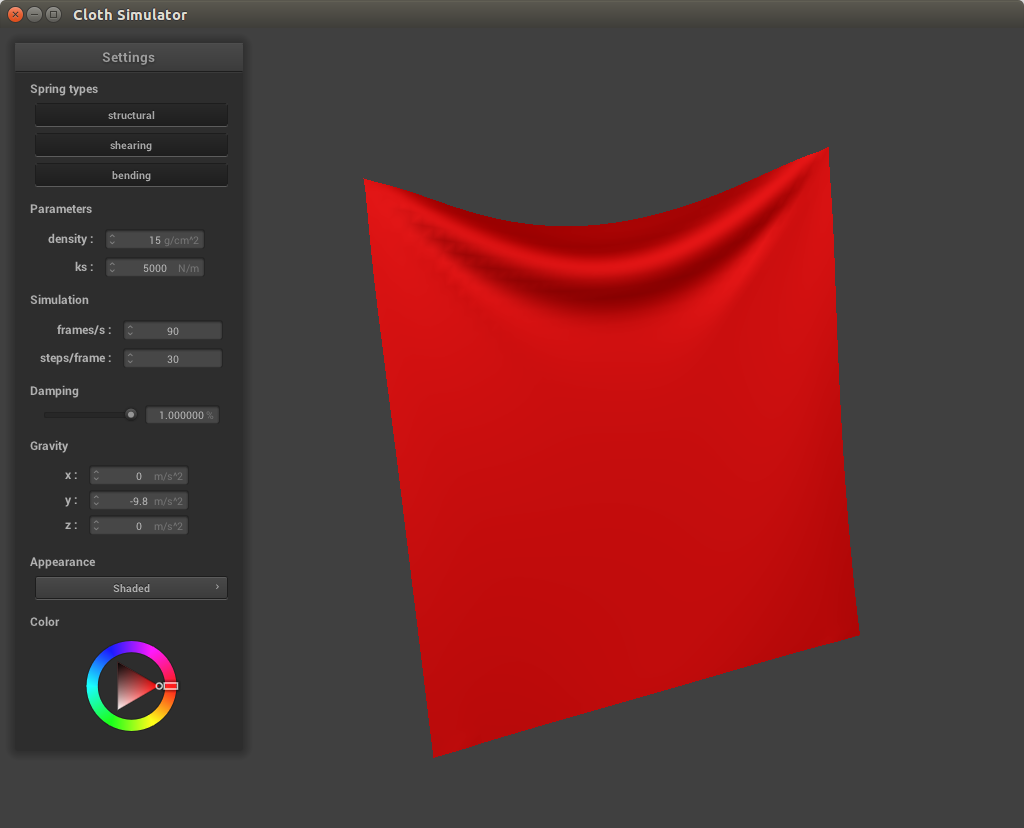
Below is the cloth with its four corners pinned.

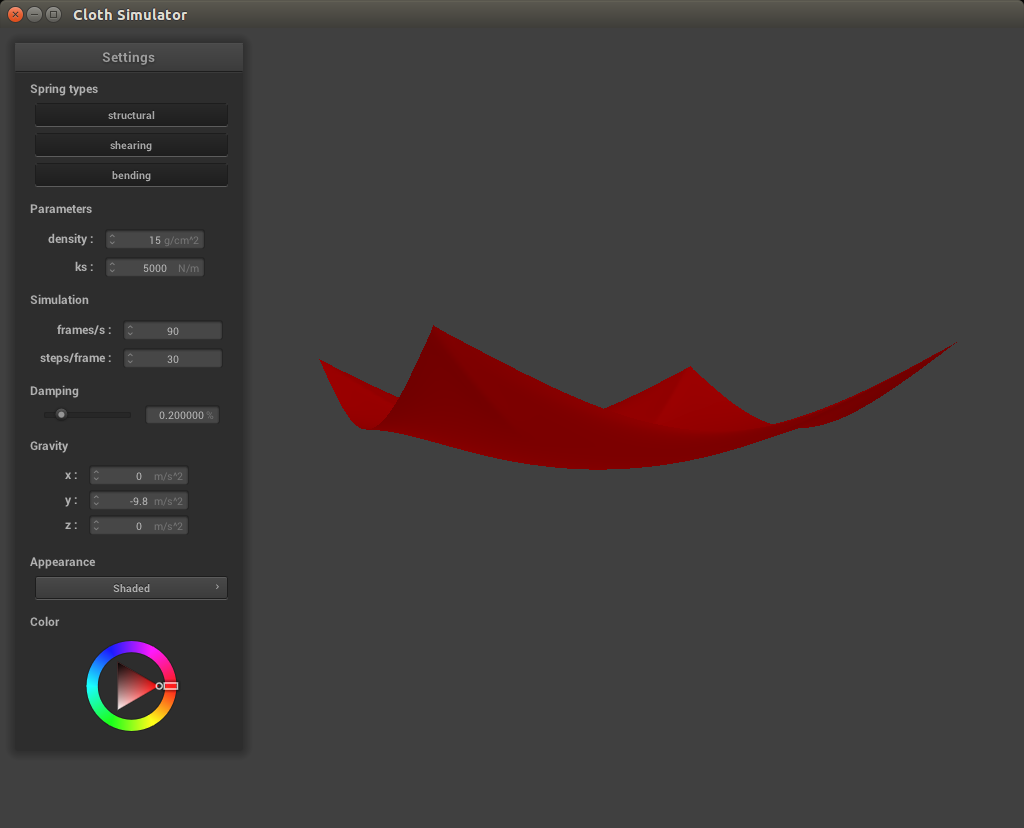
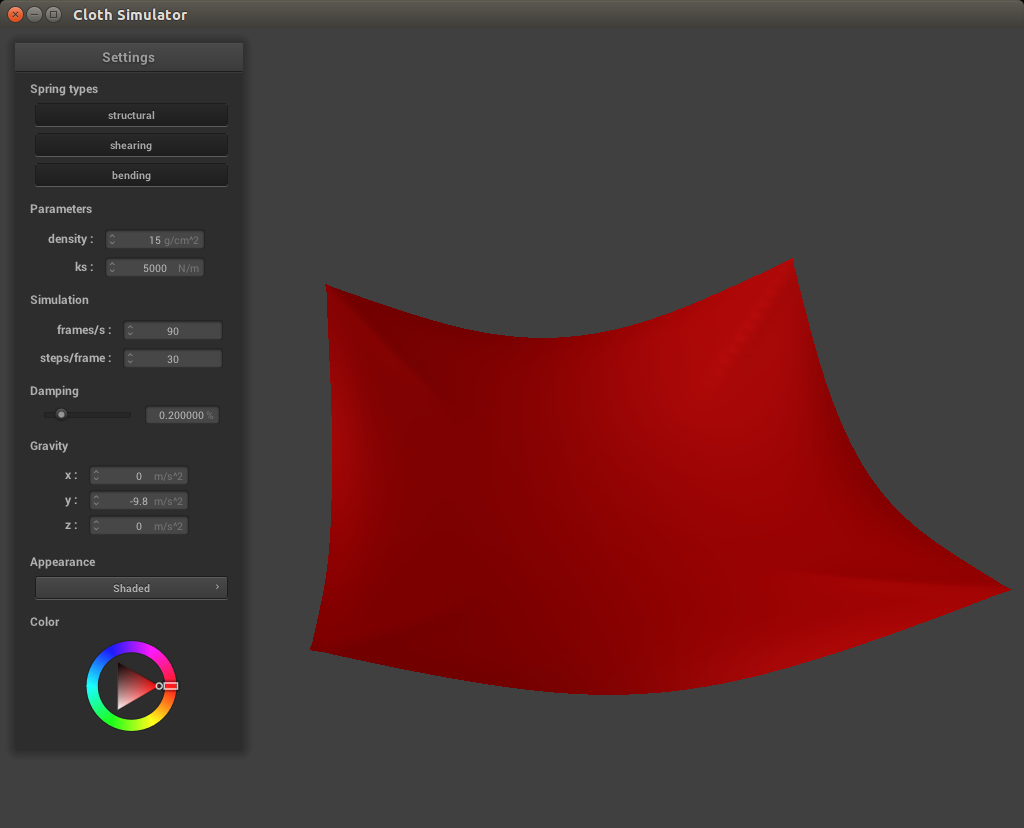
Part 3: Handling collisions with other objects

In order to detect collisions with other surfaces, We need an implicit representation of their geometry. For a sphere, we check if the distance between the point mass position and the sphere's origin falls within the sphere's radius, in which case we calculate a point of intersection with the sphere by multiplying the radius by a unit vector pointing from the sphere origin to the point position. Then, we calculate the correction vector that will move our last position to the tangent point. Finally, we set the point mass position to be the correction vector, multiplied by (1 - friction), added to the last position.

As mentioned above, the spring constant is directly proportional to the strength of the force holding the points together. With lower spring force, the cloth is more slack and thus drapes more over the sphere whereas with high spring force, the cloth is more taut and looks almost as if someone has propped up the ends of the cloth rather than leave it resting over the sphere.

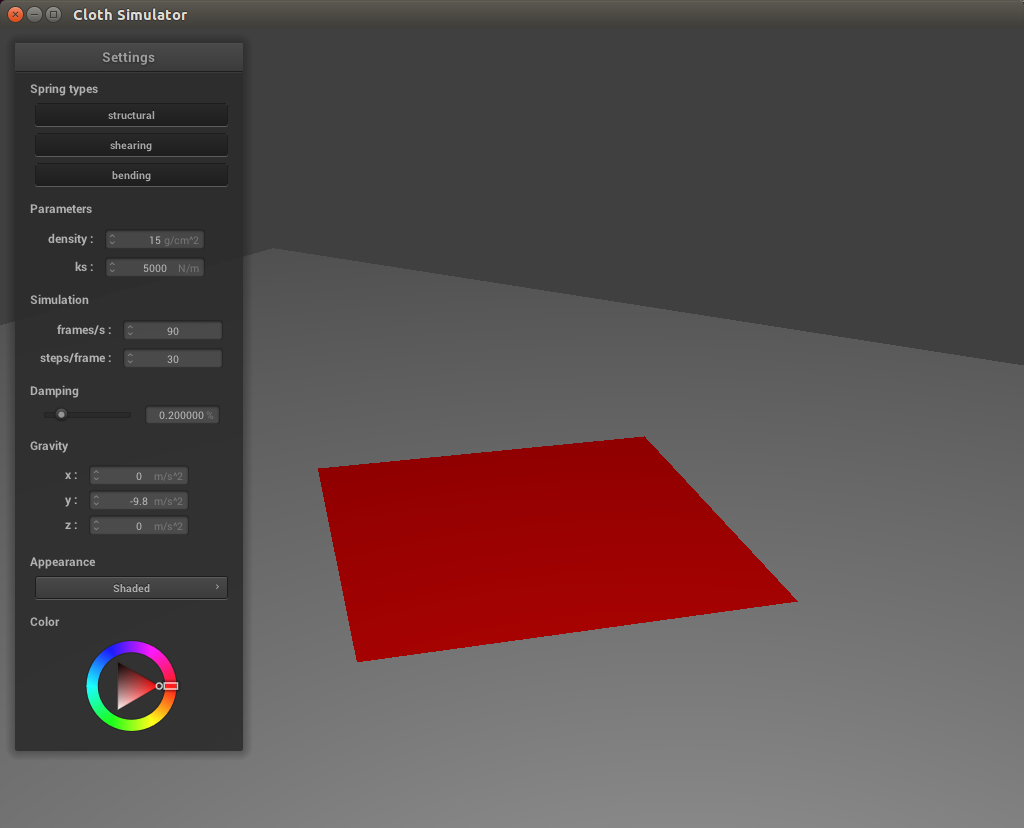
For a plane we follow a similar process. We first check if the point mass has crossed from one side of the plane to another in the time step. We do this by computing the dot product of the point mass's current position and the plane normal and comparing it to the dot product of the point mass's last position and the plane normal. If the signs changed, we know we have crossed the plane, and so we compute an intersection point for a line going straight from the current position on the plane to use as our tangent point. Once again, we calculate a correction vector that will move our last position to the tangent point and then set the point mass position to be the correction vector, multiplied by (1 - friction), added to the last position.

Part 4: Handling self-collisions

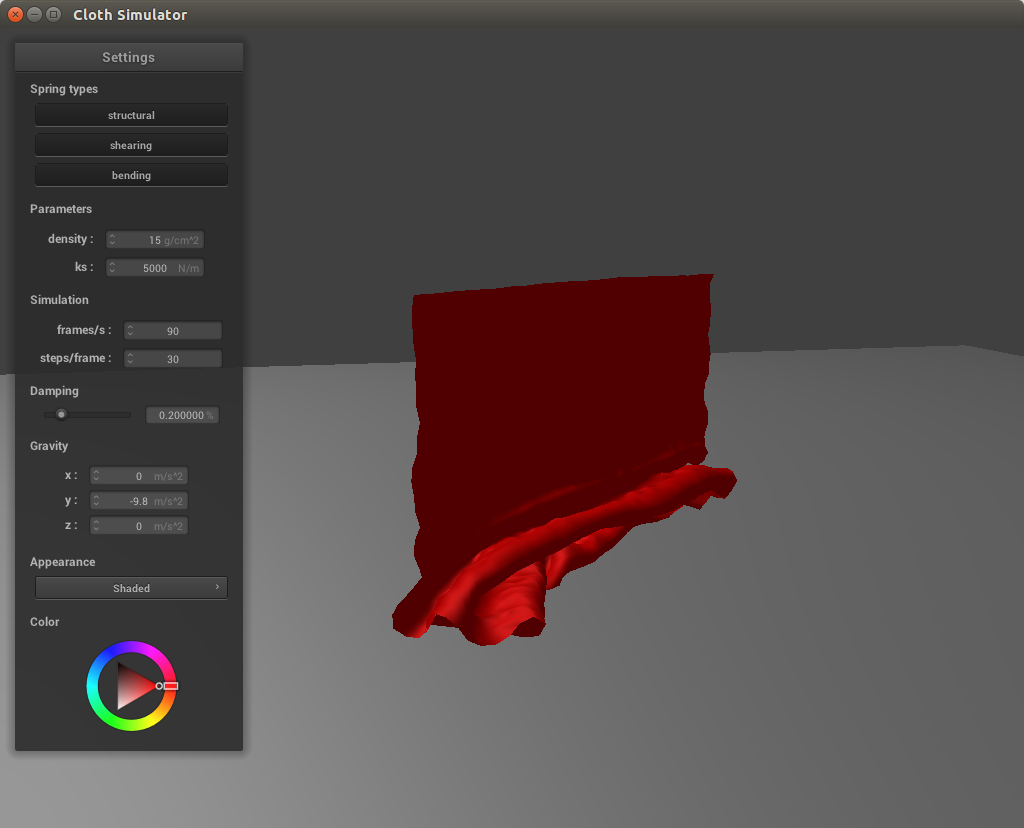
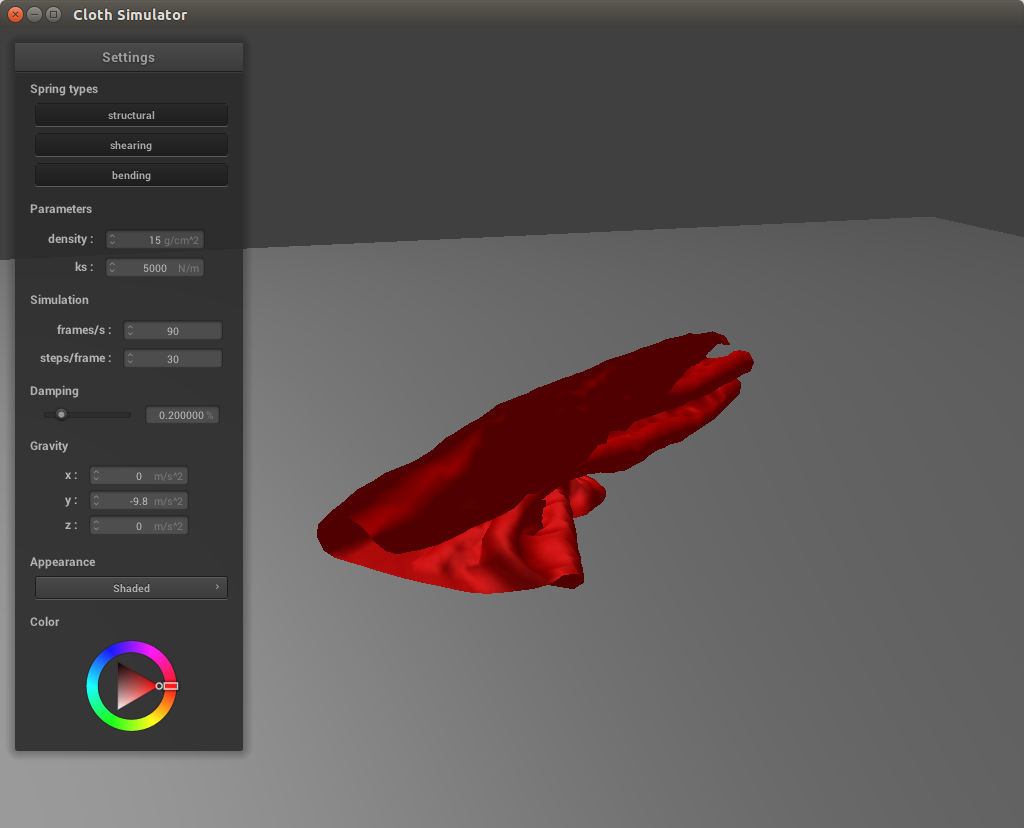
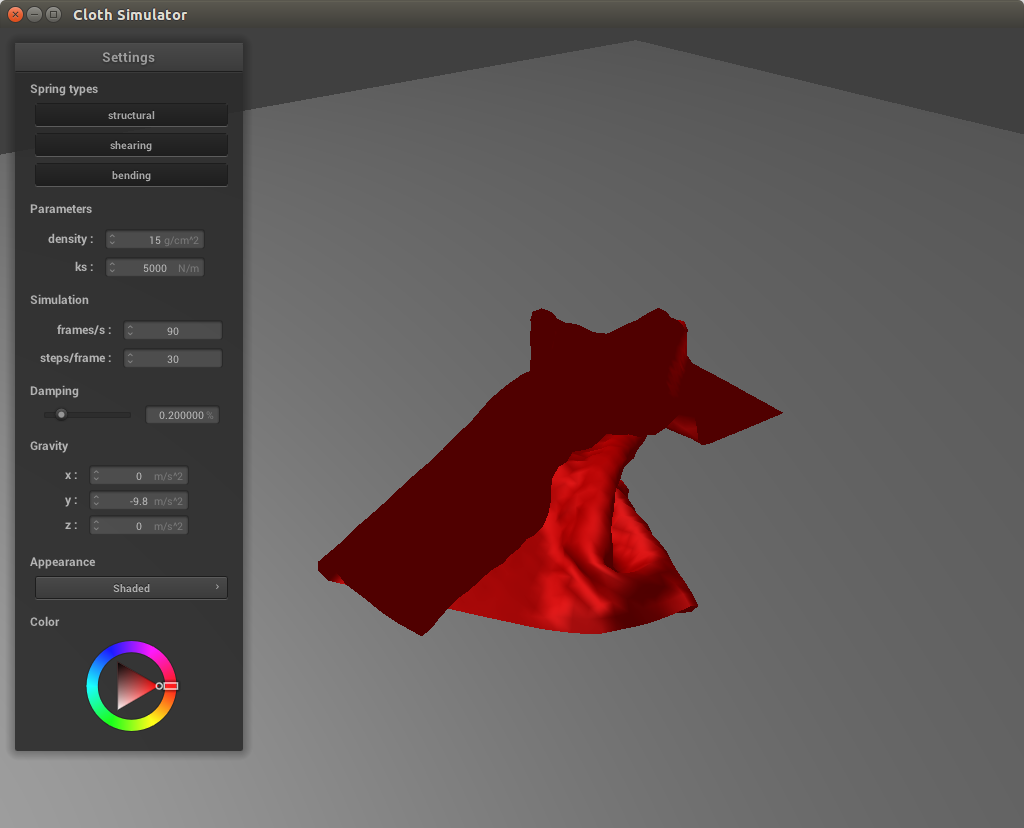
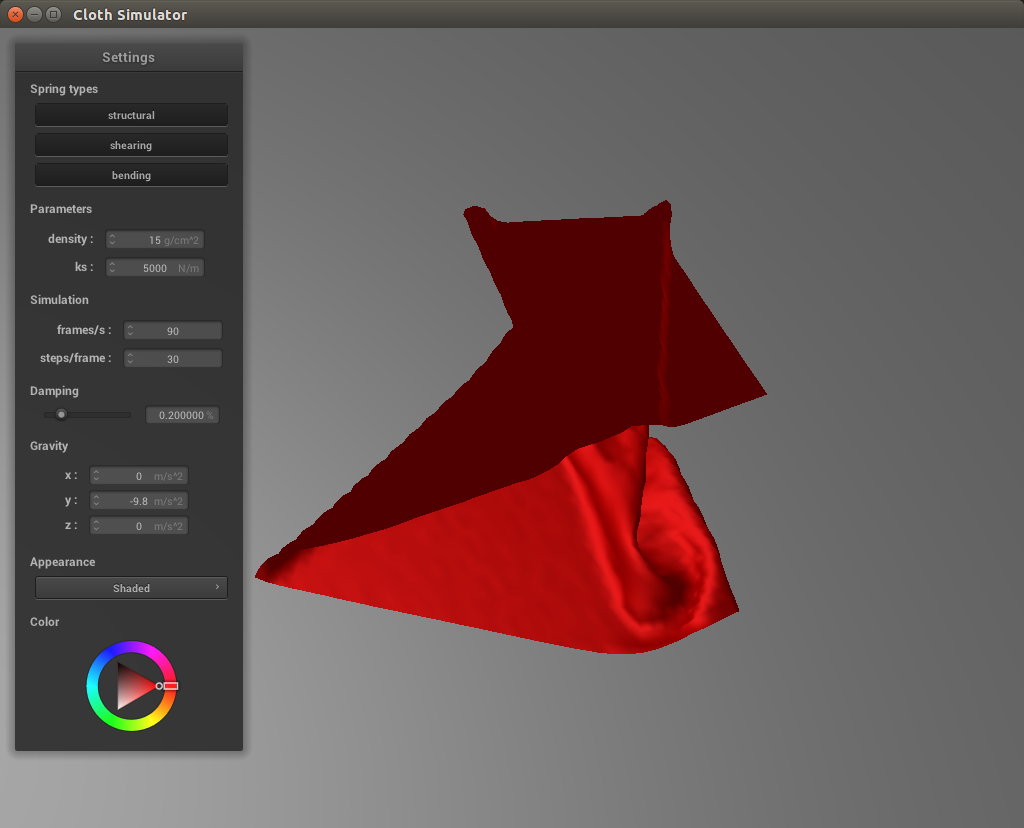
Finally, we check for instances where the cloth collides with itself. If we just iterate through each of the point masses and test them against each other, we would have rather poor performance for real time simulation, especially as the cloth becomes larger and more complex. Instead, we implement spatial hashing, mapping nearby points together. Then, as we iterate through each point mass, we simply lookup its nearby points rather than go through the entire list of point masses again. To do this, we first need to create a hash function for a particular set of coordinates. I multiplied each coordinate x, y, and z by 100 (to consider a few more digits that would have been after the decimal point) and divided them by 3 before flooring them (to group coordinates within a box together). Then, using our hashing function we populate a spatial map and then implement a collide function to check between a point and all of its nearby points. If the distance between them is less than twice the cloth thickness, we apply a correction vector only to the current point being considered, such that they are double the thickness apart.

With a higher spring constant, the cloth does not curl up as much against itself in the early stages of falling. This is due to the stronger force between the points being more resistant to changes in position. With a lower density, the cloth also will not curl as much against itself, because the particles will have a greater force exerted against them, smoothing out the cloth faster.